Transport and Heating in Radiatively Inefficient Accretion Flows
There are two modes of accretion: geometrically thin, optically
thick disks; and geometrically thick, optically thin accretion
flows. Plasma is able to cool efficiently in geometrically thin
accretion; thus heat produced by turbulent stresses is radiated
locally. In hot, dilute accretion flows the cooling time is
longer than radial advection time; plasma is hotter as the heat is
retained and not radiated. Since radiatively inefficient accretion
flows (RIAFs) are hot and dilute, they are also collisionless
at the disk size scale. The prime example of a RIAF is the radio
and
X-ray source Sgr A* in the Galactic center.
 Accretion in sufficiently ionized magnetized accretion flows
occurs because of the magnetorotational instability (MRI). MRI
in the collisionless regime, which is relevant for RIAFs, is a robust
instability. In collisionless plasma, particles freely stream
along magnetic field lines but are confined to a
Larmor radius (usually much smaller than the mean free path) in the
perpendicular direction. Pressure
is anisotropic with respect to the magnetic field lines. Since
Larmor radius is small, first adiabatic invariant (pperp/B) is
conserved.
As MRI amplifies magnetic fields, pperp becomes larger
than ppar. pperp>ppar corresponds to a viscosity which results in
viscous stress and viscous heating. In a collisional plasma viscosity
is determined by collisions (viscous stress ~ pressure/collision
frequency). However, pressure anisotropy in collisionless plasmas is
limited by gyroradius scale instabilities: firehose for ppar>pperp;
and mirror, ion-cyclotron, and electron-whistler instabilities for
pperp>ppar. Pressure anisotropy is such that the viscous (anisotropic)
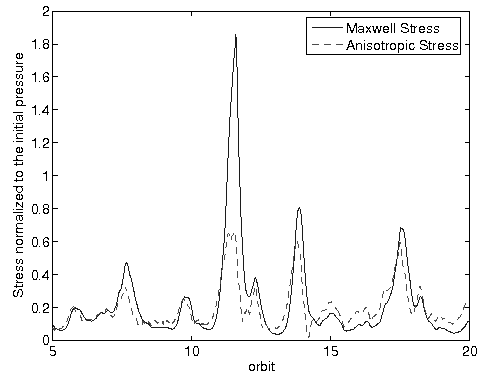
stress is comparable to the Maxwell stress (see the Fig. on right), and may even
dominate if the ratio of plasma pressure and magnetic pressure is >>1.
Accretion in sufficiently ionized magnetized accretion flows
occurs because of the magnetorotational instability (MRI). MRI
in the collisionless regime, which is relevant for RIAFs, is a robust
instability. In collisionless plasma, particles freely stream
along magnetic field lines but are confined to a
Larmor radius (usually much smaller than the mean free path) in the
perpendicular direction. Pressure
is anisotropic with respect to the magnetic field lines. Since
Larmor radius is small, first adiabatic invariant (pperp/B) is
conserved.
As MRI amplifies magnetic fields, pperp becomes larger
than ppar. pperp>ppar corresponds to a viscosity which results in
viscous stress and viscous heating. In a collisional plasma viscosity
is determined by collisions (viscous stress ~ pressure/collision
frequency). However, pressure anisotropy in collisionless plasmas is
limited by gyroradius scale instabilities: firehose for ppar>pperp;
and mirror, ion-cyclotron, and electron-whistler instabilities for
pperp>ppar. Pressure anisotropy is such that the viscous (anisotropic)
stress is comparable to the Maxwell stress (see the Fig. on right), and may even
dominate if the ratio of plasma pressure and magnetic pressure is >>1.
 In addition to providing stress which facilitates angular momentum transport,
pressure anisotropy also results in viscous heating (~shearing rate X pressure
anisotropy). In collisional plasma viscous heating of protons is ~40 times
larger than that of electrons, but in the collisionless regime pressure anisotropy
and hence viscous heating due to small scale instabilities is comparable for
both electron and protons. The electron to ion heating ratio (~sqrt[Te/Tp])
calculated from local shearing box simulations can be used in a 1-D model
with electron cooling (due to synchrotron and inverse-Compton) and heating
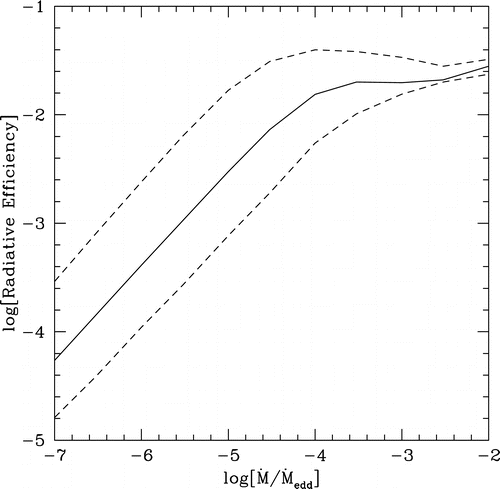
(due to viscous stress) to calculate radiative efficiency as a function of
mass accretion rate (see the Fig. on left). For Sgr A* with Bondi accretion rate ~
1e-4 Eddington rate, one obtains a radiative efficiency of ~1e-3 and a
suppression of mass accretion rate by ~1e-2 relative to Bondi, to account for
the observed dimness by ~1e-5 compared to the Bondi value. This is consistent
with many observations such as the Faraday Rotation measure.
In addition to providing stress which facilitates angular momentum transport,
pressure anisotropy also results in viscous heating (~shearing rate X pressure
anisotropy). In collisional plasma viscous heating of protons is ~40 times
larger than that of electrons, but in the collisionless regime pressure anisotropy
and hence viscous heating due to small scale instabilities is comparable for
both electron and protons. The electron to ion heating ratio (~sqrt[Te/Tp])
calculated from local shearing box simulations can be used in a 1-D model
with electron cooling (due to synchrotron and inverse-Compton) and heating
(due to viscous stress) to calculate radiative efficiency as a function of
mass accretion rate (see the Fig. on left). For Sgr A* with Bondi accretion rate ~
1e-4 Eddington rate, one obtains a radiative efficiency of ~1e-3 and a
suppression of mass accretion rate by ~1e-2 relative to Bondi, to account for
the observed dimness by ~1e-5 compared to the Bondi value. This is consistent
with many observations such as the Faraday Rotation measure.
References:
Transition from Collisionless to Collisional Magnetorotational Instability
Shearing Box Simulations of the MRI in a Collisionless Plasma
Electron Heating in Hot Accretion Flows
 Accretion in sufficiently ionized magnetized accretion flows
occurs because of the magnetorotational instability (MRI). MRI
in the collisionless regime, which is relevant for RIAFs, is a robust
instability. In collisionless plasma, particles freely stream
along magnetic field lines but are confined to a
Larmor radius (usually much smaller than the mean free path) in the
perpendicular direction. Pressure
is anisotropic with respect to the magnetic field lines. Since
Larmor radius is small, first adiabatic invariant (pperp/B) is
conserved.
As MRI amplifies magnetic fields, pperp becomes larger
than ppar. pperp>ppar corresponds to a viscosity which results in
viscous stress and viscous heating. In a collisional plasma viscosity
is determined by collisions (viscous stress ~ pressure/collision
frequency). However, pressure anisotropy in collisionless plasmas is
limited by gyroradius scale instabilities: firehose for ppar>pperp;
and mirror, ion-cyclotron, and electron-whistler instabilities for
pperp>ppar. Pressure anisotropy is such that the viscous (anisotropic)
stress is comparable to the Maxwell stress (see the Fig. on right), and may even
dominate if the ratio of plasma pressure and magnetic pressure is >>1.
Accretion in sufficiently ionized magnetized accretion flows
occurs because of the magnetorotational instability (MRI). MRI
in the collisionless regime, which is relevant for RIAFs, is a robust
instability. In collisionless plasma, particles freely stream
along magnetic field lines but are confined to a
Larmor radius (usually much smaller than the mean free path) in the
perpendicular direction. Pressure
is anisotropic with respect to the magnetic field lines. Since
Larmor radius is small, first adiabatic invariant (pperp/B) is
conserved.
As MRI amplifies magnetic fields, pperp becomes larger
than ppar. pperp>ppar corresponds to a viscosity which results in
viscous stress and viscous heating. In a collisional plasma viscosity
is determined by collisions (viscous stress ~ pressure/collision
frequency). However, pressure anisotropy in collisionless plasmas is
limited by gyroradius scale instabilities: firehose for ppar>pperp;
and mirror, ion-cyclotron, and electron-whistler instabilities for
pperp>ppar. Pressure anisotropy is such that the viscous (anisotropic)
stress is comparable to the Maxwell stress (see the Fig. on right), and may even
dominate if the ratio of plasma pressure and magnetic pressure is >>1.
 In addition to providing stress which facilitates angular momentum transport,
pressure anisotropy also results in viscous heating (~shearing rate X pressure
anisotropy). In collisional plasma viscous heating of protons is ~40 times
larger than that of electrons, but in the collisionless regime pressure anisotropy
and hence viscous heating due to small scale instabilities is comparable for
both electron and protons. The electron to ion heating ratio (~sqrt[Te/Tp])
calculated from local shearing box simulations can be used in a 1-D model
with electron cooling (due to synchrotron and inverse-Compton) and heating
(due to viscous stress) to calculate radiative efficiency as a function of
mass accretion rate (see the Fig. on left). For Sgr A* with Bondi accretion rate ~
1e-4 Eddington rate, one obtains a radiative efficiency of ~1e-3 and a
suppression of mass accretion rate by ~1e-2 relative to Bondi, to account for
the observed dimness by ~1e-5 compared to the Bondi value. This is consistent
with many observations such as the Faraday Rotation measure.
In addition to providing stress which facilitates angular momentum transport,
pressure anisotropy also results in viscous heating (~shearing rate X pressure
anisotropy). In collisional plasma viscous heating of protons is ~40 times
larger than that of electrons, but in the collisionless regime pressure anisotropy
and hence viscous heating due to small scale instabilities is comparable for
both electron and protons. The electron to ion heating ratio (~sqrt[Te/Tp])
calculated from local shearing box simulations can be used in a 1-D model
with electron cooling (due to synchrotron and inverse-Compton) and heating
(due to viscous stress) to calculate radiative efficiency as a function of
mass accretion rate (see the Fig. on left). For Sgr A* with Bondi accretion rate ~
1e-4 Eddington rate, one obtains a radiative efficiency of ~1e-3 and a
suppression of mass accretion rate by ~1e-2 relative to Bondi, to account for
the observed dimness by ~1e-5 compared to the Bondi value. This is consistent
with many observations such as the Faraday Rotation measure.