Spherical Accretion With Anisotropic Thermal Conduction
A useful model for accretion by a point mass surrounded by a uniform plasma is given by Bondi accretion, a solution
of Euler equations in 1-D with subsonic and supersonic flows at the outer and inner boundaries, respectively. This
solution is very similar to Parker's solar wind solution with a sonic point, except that it is an inflow rather
than an outflow. In compact objects with a surface, e.g., neutron stars and white dwarfs, spherical accretion flow
transitions to a boundary layer where supersonic plasma is brought to rest as it hits the surface of the compact
object. However, in black holes, which have no material boundary, supersonic material can smoothly fall through the
even horizon carrying its energy and angular momentum with it. While this is true in the absence of magnetic
fields, MHD simulations show that magnetic dissipation disturbs the smooth supersonic inflow and resistive heating
reduces the mass accretion rate by 10-100 with respect to the Bondi rate.
We carried out numerical simulations of an initial Bondi accretion flow in presence of an initially weak vertical
magnetic field, with thermal conduction along magnetic field lines. We try two sets of runs: r>~ Bondi radius,
and r<< Bondi radius. The large radius simulation, where the inflow time is longer than the buoyancy time, shows magnetic
field reorientation due to the magnetothermal instability (MTI), a buoyancy instability driven by negative temperature
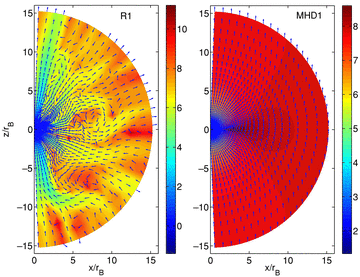
gradient. MTI changes magnetic geometry to be primarily radial (see Fig. on right), such that the growth rate of the
instability becomes negligibly small in the saturated state. The Fig. on right shows plasma beta and magnetic field unit vectors after many
buoyancy times for run with and without anisotropic conduction; while the plasma is almost still in absence of anisotropic
conduction, with anisotropic conduction MTI reorients magnetic fields. 
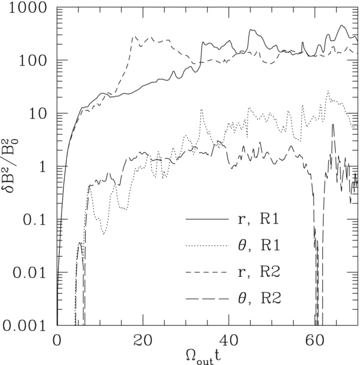Since magnetic field lines are just reoriented, saturated magnetic field energy is proportional to the initial magnetic
energy (i.e., magnetic field saturation is quasilinear;
see Fig. on left). The Fig. on left shows volume averaged saturated magnetic energy (r & theta components) scaled
to initial magnetic energy as a function of time for two runs which differ in magnitude of initial field strength by 10;
field strength is quite weak so that magnetic tension is negligible. Figure on left shows that the saturated magnetic
field strength scales with the initial field strength.
This is unlike Schwarzschild's instability in adiabatic plasmas which generates a strong convective dynamo and makes
the plasma isentropic.
Small radius (r<< Bondi radius) simulations are done separately as simulations that resolve r~ Schwarzschild radius and
r~ Bondi radius are numerically quite challenging. Temperature is held fixed at the virial temperature at the outer boundary (256
Schwarzschild radii). Initially supersonic inflow amplifies fields and leads to magnetic dissipation of oppositely directed
magnetic field lines.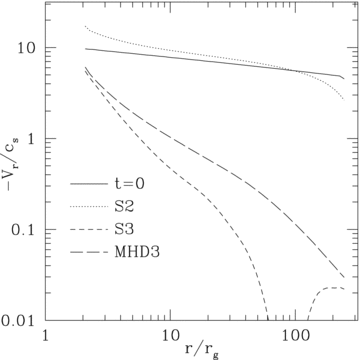 
Local heating increases the
temperature and flow remains supersonic only within few Schwarzschild radii (Fig. on right). The Fig. on right shows inflow
Mach number as a function of radius at late times for hydro (dotted line), MHD (long dashed line), and MHD with anisotropic
conduction (short dashed line) runs. While plasma inflow is roughly at free-fall rate in hydro, magnetic dissipation reduces
net infall velocity; thermal conduction that brings heat out to larger radii further reduces radial infall velocity.
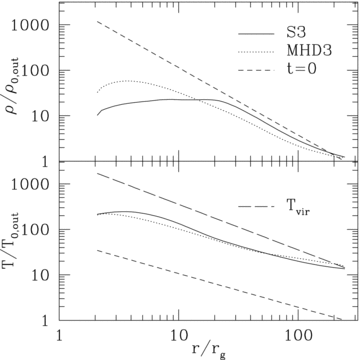The Fig. on left shows angle averaged density and
temperature profiles as a function of radius for the MHD run, and the MHD run with conduction. Density in inner regions is flattened
such that mass flux (~r^2 d v_r) is constant; thus, S3 with steeper velocity profile has a shallower density profile. The temperature
is slightly sub-virial but much hotter than the initial Bondi solution. Mass accretion rate is reduced by local magnetic
dissipation and heating due to thermal conduction. There is no evidence for outward convective transport of energy, although
there are strong turbulent velocities driven by magnetic dissipation.
Reference:
Spherical accretion with anisotropic thermal conduction