Multifractality in graphene

Multifractal conductance fluctuations at the plateau-to-plateau transition of QHE (Accepted in PRL):
In mesoscopic high-mobility graphene devices, we studied the statistics of conductance in the quantum Hall regime during quantum Hall plateau-to-plateau (PPT) transitions. We observe reproducible mesoscopic fluctuations in Hall conductance in high-mobility graphene devices. The scaling properties of these fluctuations near the quantum Hall critical points are multifractal. This multifractality rapidly suppressed as the chemical potential of the system moves away from these critical points, or as the temperature was increased. Our experiments and analysis suggest that the multifractality of conductance fluctuations results from localization-delocalization transitions occurring at critical points. This provides a new framework to probe into the criticality of the localization-delocalization transitions, via transport measurements.
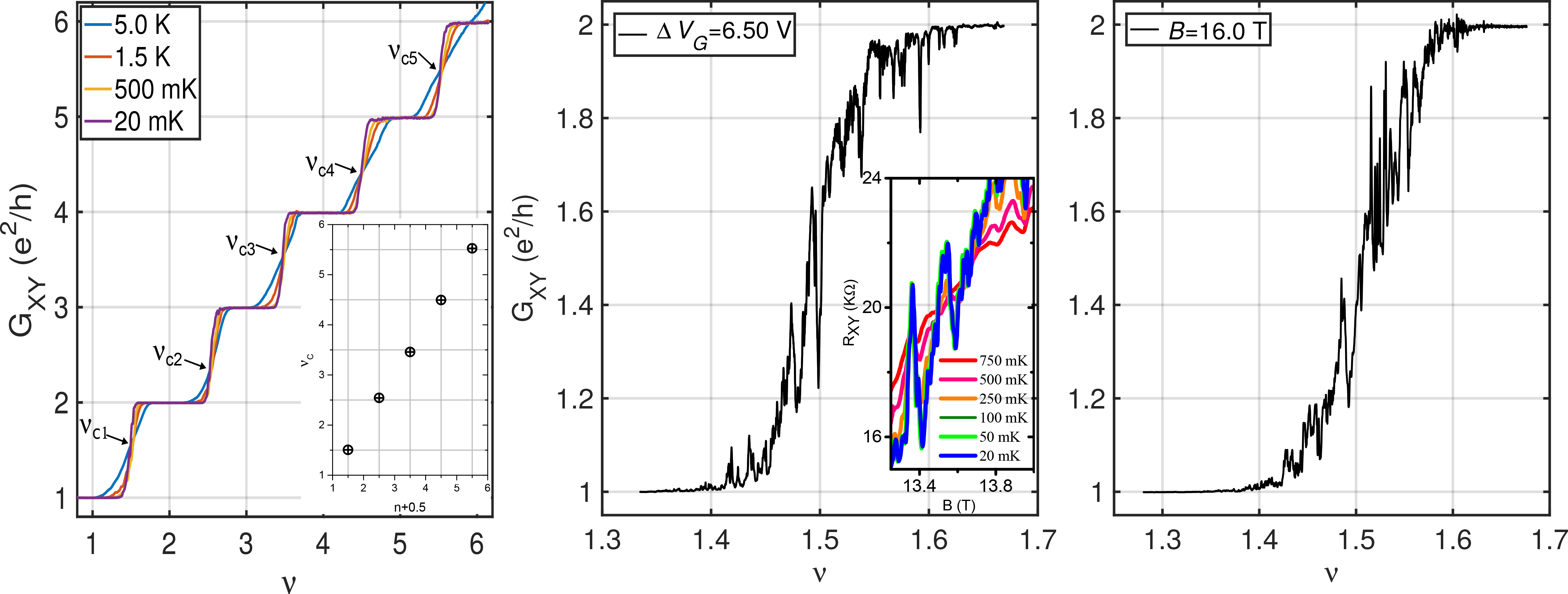
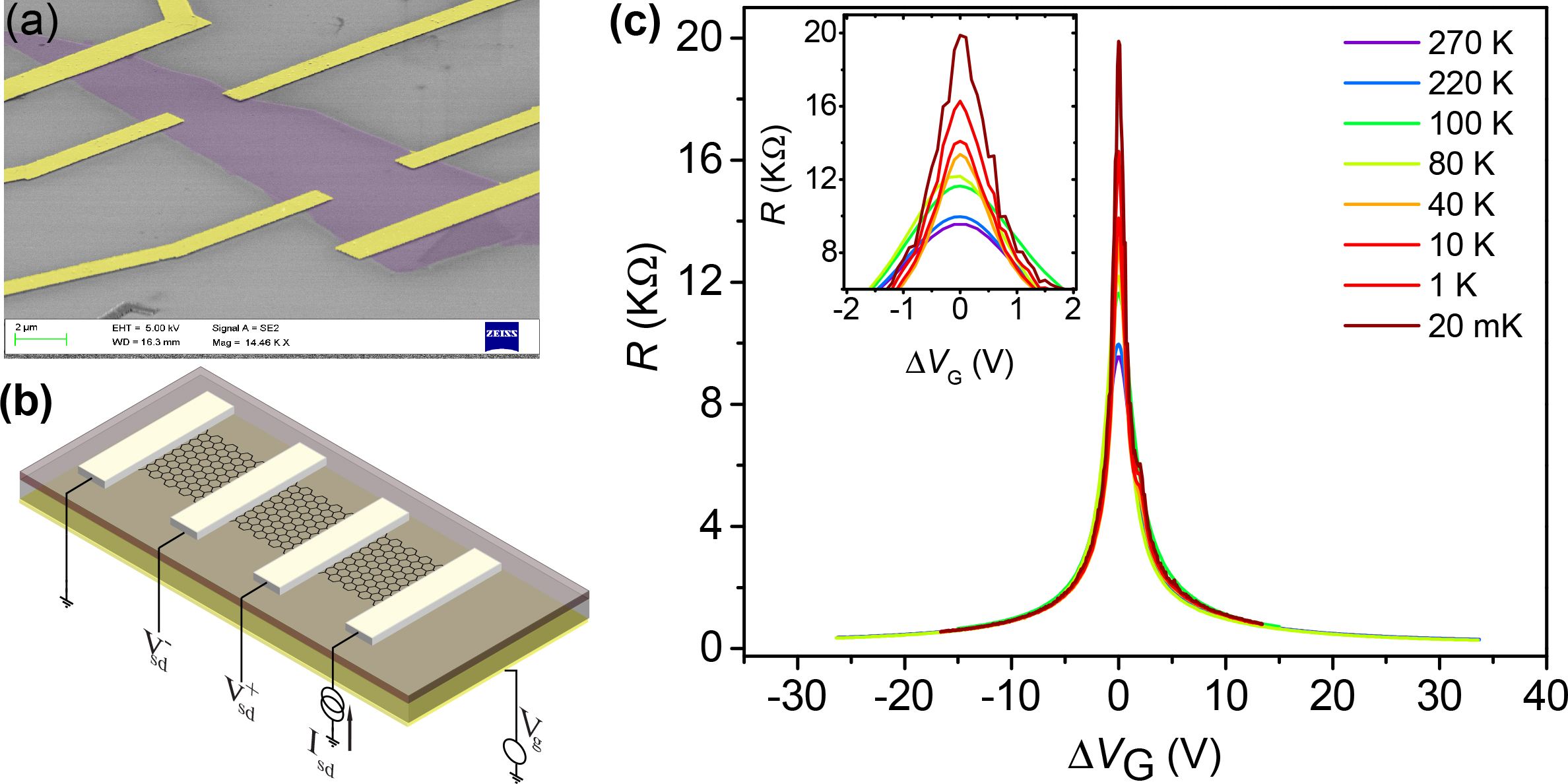
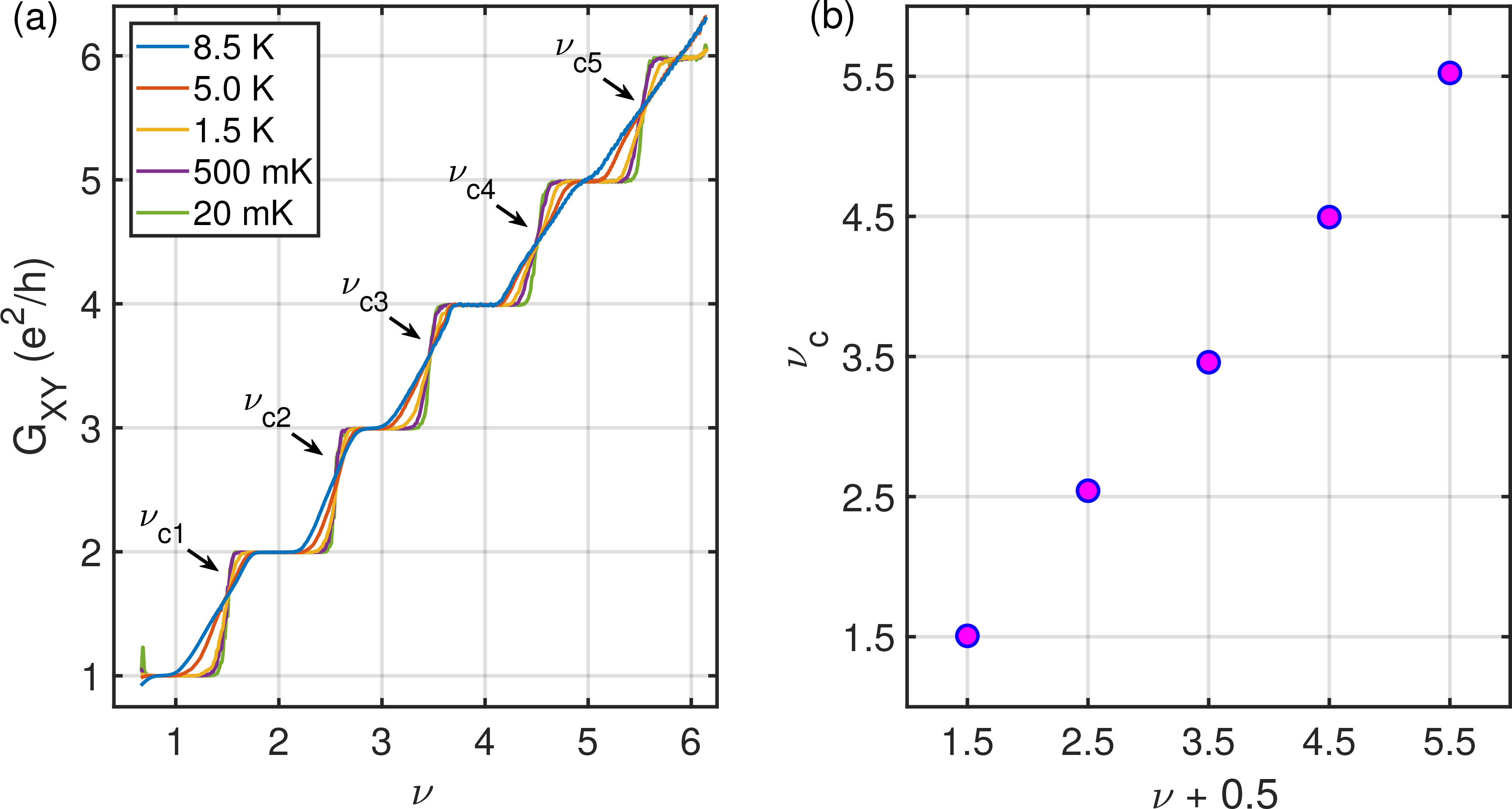
We have investigated quantum Hall plateau-to-plateau transitions at different temperatures, from 20~mK to 10~K, in high mobility hBN-encapsulated graphene van der Waals heterostructure devices. We have observed perfect power-law scaling with universal critical exponent k=0.42, for plateau-to-plateau transitions between different broken-symmetry states. Our experiments show that the non-universality of quantum Hall transitions in graphene reported previously were effects of long-range charge impurity scattering. Suppression of charge impurity scattering restores the Anderson localization transition.
Multifractal conductance fluctuations and Anderson localization Nature Comm. Phys. 1, 1 (2018).
In quantum systems, signatures of multifractality are rare. They have been found only in the multiscaling of eigenfunctions at critical points. Here we demonstrate multifractality in the magnetic-field-induced universal conductance fluctuations of the conductance in a quantum condensed-matter system, namely, high-mobility single-layer graphene field-effect transistors. This multifractality decreases as the temperature increases or as doping moves the system away from the Dirac point. Our measurements and analysis present evidence for an incipient Anderson localization near the Dirac point as the most plausible cause for this multifractality. Our experiments suggest that multifractality in the scaling behavior of local eigenfunctions is reflected in macroscopic transport coefficients. We conjecture that an incipient Anderson-localization transition may be the origin of this multifractality. It is possible that multifractality is ubiquitous in the transport properties of low-dimensional systems. Indeed, our work suggests that we should look for multifractality in transport in other low-dimensional quantum condensed-matter systems.