We explore several frontiers of the quantum theory of condensed matters and materials sciences. In a broad sense, our research interests lie in understanding and predicting materials properties driven by quantum phenomena that are amenable to experimental verifications and device implementations. More specifically, we study superconductivity, emergent correlated phases, topological phases of matter, and non-Hermitian quantum properties. The techniques we use in our group include analytical models, density-functional theory (DFT), momentum-resolved density fluctuation (MRDF) theory (homemade code), and numerical simulation, among others.
Research Highlights

Many systems, such as open quantum systems, systems out of equilibrium, disordered systems, etc, are describable by non-Hermitian Hamiltonians. However, the quantum theory of non-Hermitian Hamiltonians is not well developed due to the lack of a properly defined Hilbert space and unitary time evolution. We are working on many aspects of this theoretical developments at the fundamental level.
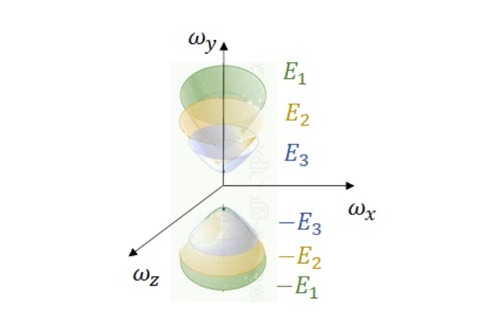

One of the fascinating facts about superconductivity is that despite more than 100 years of extensive research and 7 Nobel prizes, plenty of surprises is discovered daily. We have been interested in the theoretical studies of conventional and unconventional superconductivity and the interplay of superconductivity with other phases. We often study the the pairing symmetry and pairing mechanism of superconductivity and its competition and coexistence with other exotic phases of matter. We are also interested in studying topological superconductivity.
Recent Highlights
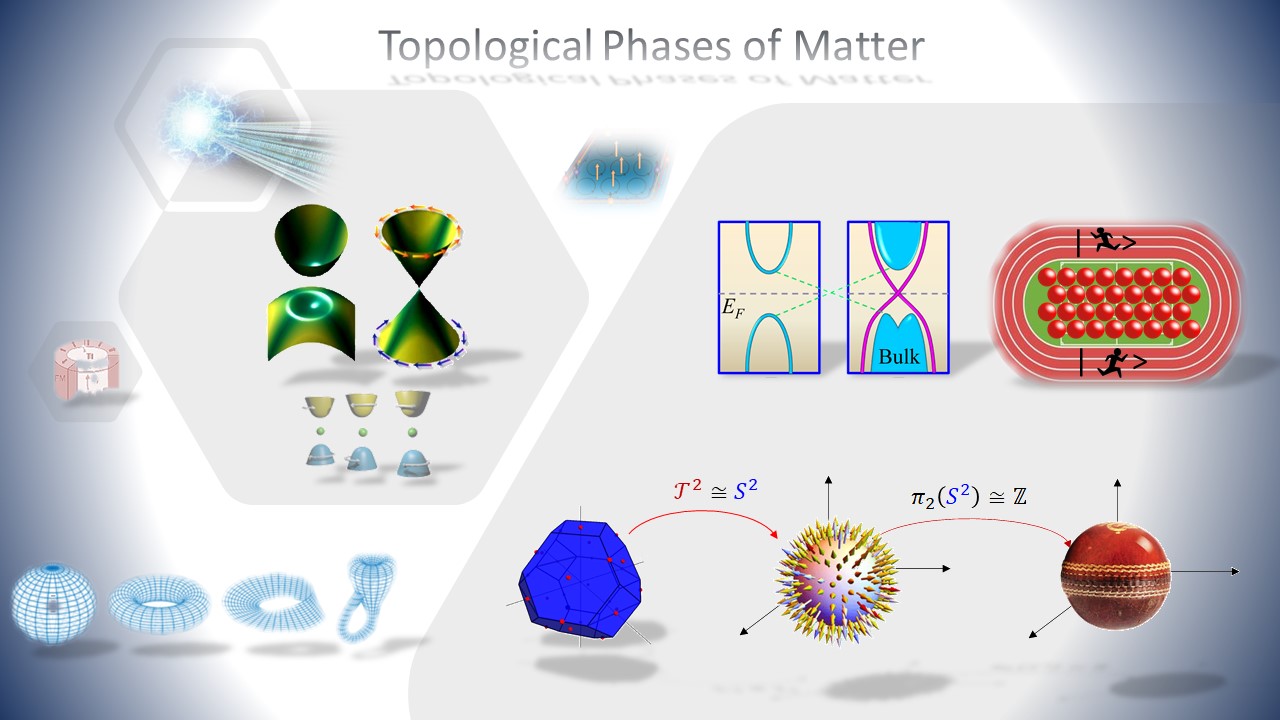
Roughly speaking, a topological space is a set of points with a sense of continuity between the points, so that it takes a shape which is deformable to another shape without removing any points. Consequently, most of the physical processes, trajectories, patterns are formed in topological spaces. In quantum condensed matter field, it is a new realization that the Hamiltonians’ parameter space can be a topological space - with interesting physical properties such as quantised Hall transport, fractional particles, entanglement, and electromagnetic responses. We study such physics in both electronic structures, spin textures, and Moire lattices.
Recent Highlights
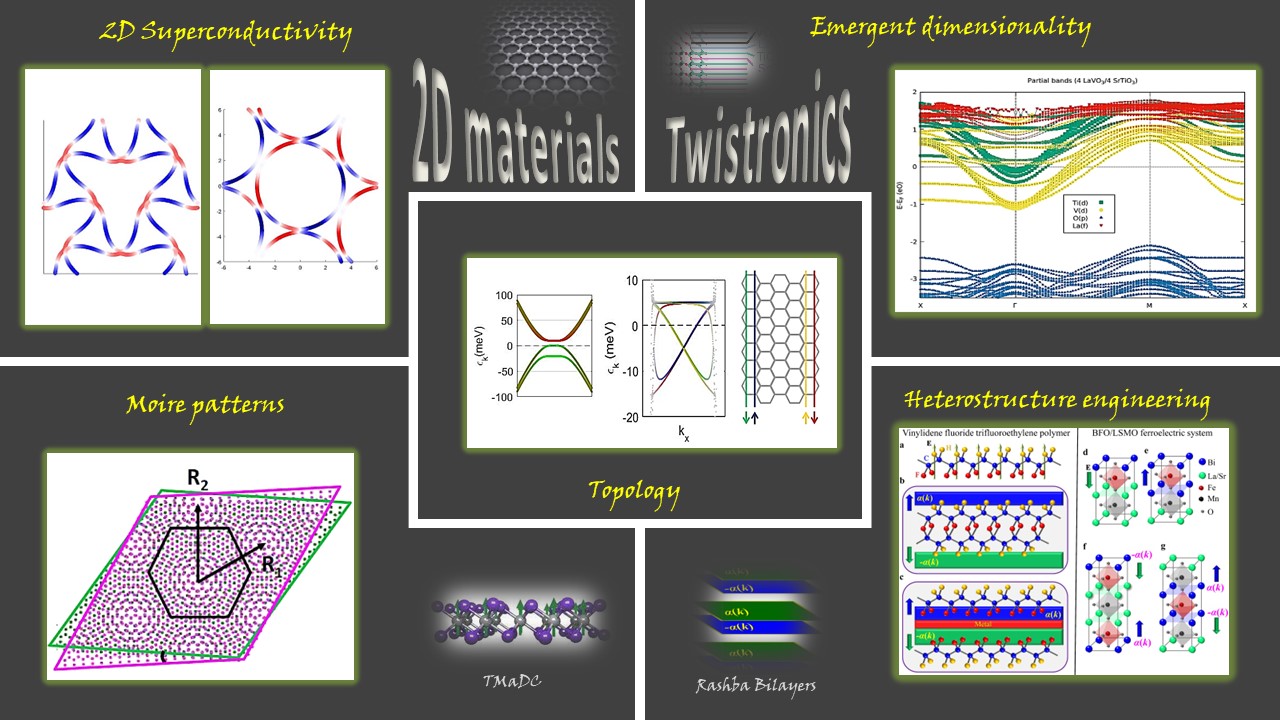
Physics can be drastically different in different dimensions even for the same Hamiltonian. The door to two dimensional materials was opened by graphene, which followed transitional metal dichalcogenides, Kagome materials and now we have 2D magnets. The symmetry classification changes, the correlation effect is enhanced, and electronic, magnetic, optical, superconducting and topological properties are intertwinned. Materials have the blessing and curse of periodicity of atoms, which provide an abundance of symmetries, but at the same time, constraint the possibility of phases. Twisted bilayer systems are a modern technology which allows to dissolve or divert these disadvantages and we can possibly realize anything and everything.
Recent Highlights
In going beyond typical mean-field solutions, solitons, emergent gauge/curvature fields, fractionalization/fragmentation, entanglement are presently sought in a variety of setups. Governing such phases require additional materials help, such as geometric frustration, reduced symmetry, chiral interactions, and topology. Cold atoms, photonics systems also can simmulate such lattice.
Recent Highlights

As atoms are arranged in periodic lattices, the orbital wavefunctions of electrons change to Bloch wavefunctions. So they do not remain to be the same electrons, rather become collective excitations which we call quasiparticles. When electron-electron interaction is included, the properties of quasiparticles can drastically change, including the definition of quasiparticles itself. New phenomena such as non-Fermi liquid, strange metal, Mott insulator emerges, which proximitise the unconventional superconductivity, competing orders to more exotic states. In fact, one amay govern even novel excitations, which can be fermionic, bosonic or even more exotic in nature.
The numerical code for the intermediate coupling model is dubbed ‘momentum-resolved density fluctuation (MRDF)’ code.